Draw Circle in Complex Plane

Circumvolve with radius of ane

Illustration of a unit of measurement circle. The variable t is an bending measure.

Animation of the act of unrolling the circumference of a unit circle, a circle with radius of 1. Since C = 2πr , the circumference of a unit circle is 2π.

In mathematics, a unit circumvolve is a circle of unit radius—that is, a radius of 1.^[i] Frequently, especially in trigonometry, the unit of measurement circumvolve is the circle of radius ane centered at the origin (0, 0) in the Cartesian coordinate system in the Euclidean plane. In topology, it is ofttimes denoted as S ⁱ because it is a one-dimensional unit n -sphere.^{[2] [note 1]}

If (x, y) is a signal on the unit of measurement circle's circumference, then | ten | and | y | are the lengths of the legs of a correct triangle whose hypotenuse has length 1. Thus, past the Pythagorean theorem, x and y satisfy the equation

$${\displaystyle x^{2}+y^{2}=1.}$$

Since x ⁱⁱ = (−x)² for all x , and since the reflection of whatever signal on the unit of measurement circle well-nigh the x - or y -axis is also on the unit circle, the in a higher place equation holds for all points (ten, y) on the unit circle, not only those in the first quadrant.

The interior of the unit of measurement circumvolve is called the open unit disk, while the interior of the unit circumvolve combined with the unit of measurement circle itself is called the closed unit disk.

One may also use other notions of "distance" to define other "unit circles", such equally the Riemannian circle; run across the commodity on mathematical norms for additional examples.

In the complex plane [edit]

The unit circle tin be considered equally the unit circuitous numbers, i.e., the set of complex numbers z of the form

$${\displaystyle z=due east^{it}=\cos t+i\sin t=\operatorname {cis} (t)}$$

for all t (see also: cis). This relation represents Euler'southward formula. In quantum mechanics, this is referred to equally the phase factor. It can also be defined as the fix of complex numbers satisfying

$${\displaystyle |z|=1.}$$

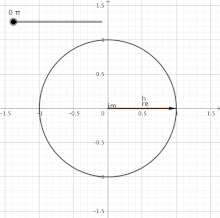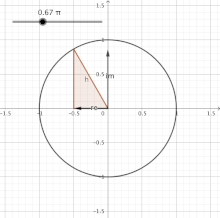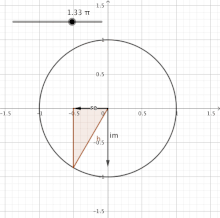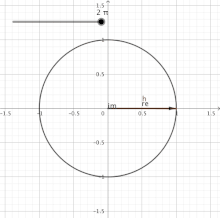
Blitheness of the unit circle with angles

Trigonometric functions on the unit circle [edit]

All of the trigonometric functions of the bending θ (theta) can be constructed geometrically in terms of a unit of measurement circle centered at O.

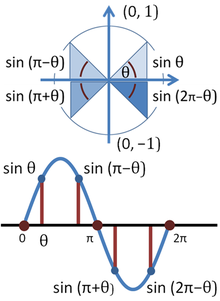
Sine function on unit circle (top) and its graph (bottom)

The trigonometric functions cosine and sine of angle θ may be defined on the unit circumvolve as follows: If (ten, y) is a signal on the unit of measurement circle, and if the ray from the origin (0, 0) to (x, y) makes an angle θ from the positive x -centrality, (where counterclockwise turning is positive), then

$${\displaystyle \cos \theta =ten\quad {\text{and}}\quad \sin \theta =y.}$$

The equation ten ² + y ² = one gives the relation

$${\displaystyle \cos ^{2}\theta +\sin ^{two}\theta =i.}$$

The unit circumvolve likewise demonstrates that sine and cosine are periodic functions, with the identities

$${\displaystyle \cos \theta =\cos(two\pi grand+\theta )}$$

$${\displaystyle \sin \theta =\sin(2\pi k+\theta )}$$

for whatsoever integer grand .

Triangles constructed on the unit circle can also be used to illustrate the periodicity of the trigonometric functions. Beginning, construct a radius OP from the origin O to a betoken P(x _i,y _ane) on the unit circle such that an angle t with 0 < t < π / 2 is formed with the positive arm of the ten -axis. Now consider a point Q(x _one,0) and line segments PQ ⊥ OQ. The upshot is a correct triangle △OPQ with ∠QOP = t . Because PQ has length y ₁ , OQ length x ₁ , and OP has length i as a radius on the unit circle, sin(t) = y _one and cos(t) = x ₁ . Having established these equivalences, have another radius OR from the origin to a point R(−x ₁,y ₁) on the circle such that the aforementioned angle t is formed with the negative arm of the x -centrality. Now consider a point S(−10 ₁,0) and line segments RS ⊥ Bone. The result is a right triangle △ORS with ∠SOR = t . It tin hence be seen that, considering ∠ROQ = π − t , R is at (cos(π − t), sin(π − t)) in the same way that P is at (cos(t), sin(t)). The conclusion is that, since (−x _one, y ₁) is the same as (cos(π − t), sin(π − t)) and (x ₁,y _ane) is the same as (cos(t),sin(t)), it is truthful that sin(t) = sin(π − t) and −cos(t) = cos(π − t). It may be inferred in a like manner that tan(π − t) = −tan(t), since tan(t) = y _one / x ₁ and tan(π − t) = y _one / −10 ₁ . A unproblematic demonstration of the higher up can be seen in the equality sin( π / four ) = sin( 3π / four ) = 1 / √2 .

When working with right triangles, sine, cosine, and other trigonometric functions simply make sense for angle measures more than nothing and less than π / 2 . However, when defined with the unit of measurement circle, these functions produce meaningful values for whatsoever real-valued angle measure – fifty-fifty those greater than 2π. In fact, all half dozen standard trigonometric functions – sine, cosine, tangent, cotangent, secant, and cosecant, equally well as archaic functions similar versine and exsecant – can be defined geometrically in terms of a unit circle, as shown at right.

Using the unit circumvolve, the values of any trigonometric function for many angles other than those labeled can exist hands calculated by paw using the bending sum and difference formulas.

Circle group [edit]

Complex numbers tin be identified with points in the Euclidean plane, namely the number a + bi is identified with the point (a, b). Nether this identification, the unit circle is a group under multiplication, called the circumvolve grouping; information technology is usually denoted ${\displaystyle \mathbb {T} .}$ On the aeroplane, multiplication by cos θ + i sin θ gives a counterclockwise rotation by θ . This group has important applications in mathematics and science.^{[ example needed ]}

Complex dynamics [edit]

Unit of measurement circle in complex dynamics

The Julia prepare of discrete nonlinear dynamical organization with evolution role:

$${\displaystyle f_{0}(x)=x^{ii}}$$

is a unit of measurement circle. Information technology is a simplest case and then it is widely used in the report of dynamical systems.

Notes [edit]

1. ^ Confusingly, in geometry a unit circle is oftentimes considered to exist a 2-sphere—not a 1-sphere. The unit circle is "embedded" in a 2-dimensional plane that contains both height and width—hence why it is called a 2-sphere in geometry. However, the surface of the circle itself is one-dimensional, which is why topologists allocate it as a one-sphere. For further give-and-take, run across the technical stardom betwixt a circle and a disk.^[2]

References [edit]

1. ^ Weisstein, Eric W. "Unit Circumvolve". mathworld.wolfram.com . Retrieved 2020-05-05 .
2. ^ ^{a b} Weisstein, Eric W. "Hypersphere". mathworld.wolfram.com . Retrieved 2020-05-06 .

See too [edit]

• Angle measure
• Pythagorean trigonometric identity
• Riemannian circumvolve
• Unit angle
• Unit of measurement disk
• Unit sphere
• Unit hyperbola
• Unit square
• Plough (unit of measurement)
• z-transform

davisliaboarpood.blogspot.com

Source: https://en.wikipedia.org/wiki/Unit_circle

Share this post